Why 3D print an origami model?
Like most families, we love to decorate our Christmas tree and have spent many happy hours making origami stars, angels and woven Danish Hearts. My favourite star has to be David Mitchell’s beautiful Electra - it’s an incredibly symmetrical model, and, unlike some modular origami models, is surprisingly robust. But, when you have children, you soon find that things get squashed or shot at with Nerf bullets :-) While straightening out Electra for the umpteenth time, I thought – why not 3D print this?
Modular Origami
Most people think of origami models as being folded from a single sheet of paper (for example, Robert J Lang’s creations), but modular origami joins lots of small, folded modules together to make a larger model that is often mathematical in style. Kunihiko Kasahara’s Origami Omnibus and David Mitchell’s Mathematical Origami are good introductions to Maths & origami. If you want to be more adventurous, then I recommend David Mitchell’s Paper Crystals, now in its second edition - “Electra” has appeared in both.
Electra - what is an Icosidodecahedron?
Electra is a skeletal polyhedral model based on the 60 edges of an icosidodecahedron – a mixture of a dodecahedron (with 12 pentagonal faces) and an icosahedron (20 triangular faces). When assembled, rings of modules dance around each other – five membered rings (pentagons) alternate with three (triangles), but never meet - except at discrete corners (and, even then, under supervision). There are also rings of ten modules forming great circles (like the equator) that run around the whole polyhedron. As you turn Electra in your hands, mirror, 2-fold, 3-fold, 5-fold and even partial 10-fold symmetry magically appears – it’s not surprising that some quasicrystals, with their forbidden 5-fold symmetry, have atoms positioned around an icosidodecahedron.
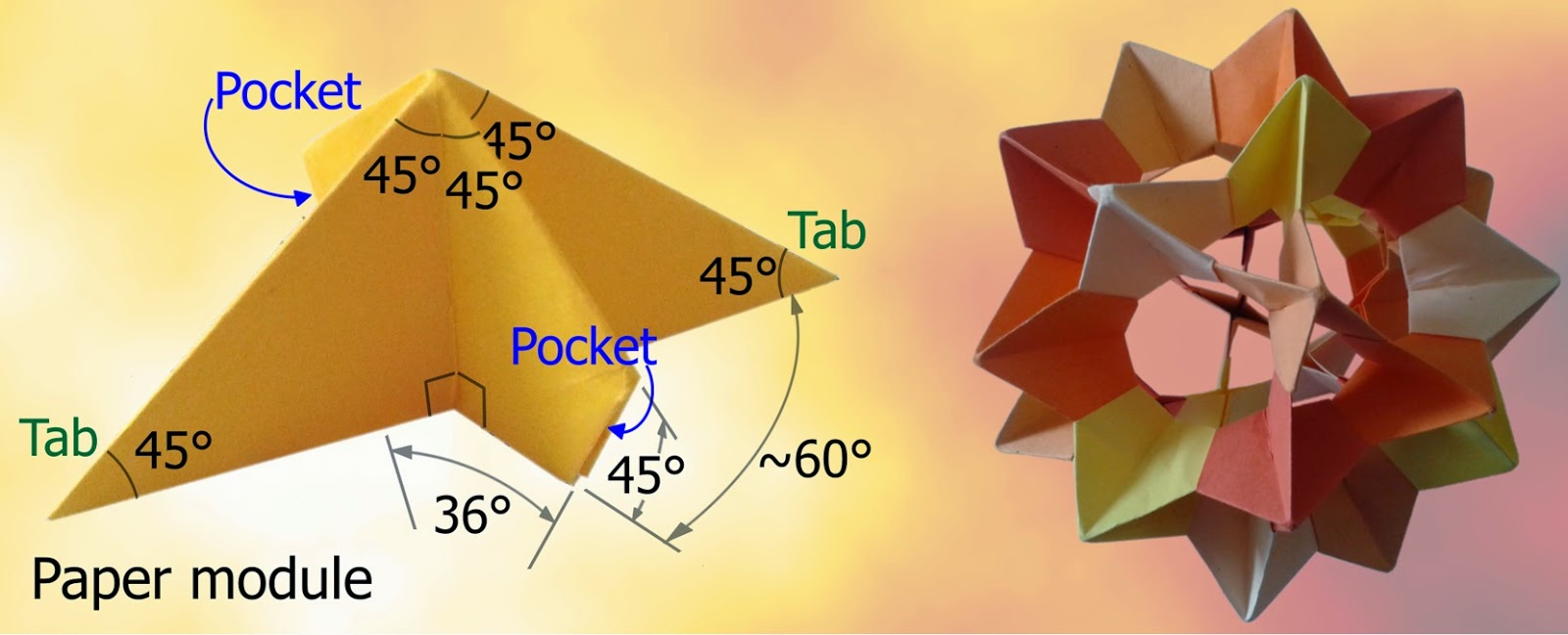
How was the 3D model designed?
I started with the X-shaped paper modules and soon found that the top point was a right angle, the tops of the tabs & pockets were at 45 degrees to the base, and the angle between the arms of the X was roughly 60 degrees. Also, ten of the modules made a ring, so the angle between the tilted ends of the pockets (for the tabs) must be 36 degrees (=360/10).
The next step was to draw it on paper and calculate the angles & lengths properly. This is where my (spherical) geometry came unstuck! Why wasn’t the X angle exactly 60 degrees? It looked to be 60 degrees, three of the modules met to make a triangle - it must be 60 degrees… It wasn’t - that little tilt between the modules made the maths “messy”.
I started trying to calculate the angle on paper, then moved to OpenSCAD, but soon gave up – it was great for designing in, but couldn’t tell me when the modules touched. Brute force and Solidworks was the approach that worked – tweaking the X angle until a ring of 5 modules and another ring of 3 modules fitted together properly. And the “60” degree angle was really 63.434957… [Or arccos(1/sqrt(5)) = arctan(2), which is 180 degrees minus the angle between the faces of a dodecahedron. Silly me for not knowing!]
The final step was to put little catches on the tabs so they locked in to a pocket on the opposite side of the module. These proved to be tricky to print, very fragile, and left horrible lumps and bumps on the outside of the module. So I experimented with smooth tabs – they worked much better. A bit more tweaking of the overall module thickness, the tab thickness (40% of this) and the pocket width (1/3) and we’re ready to print and assemble a whole model.
Assembly & colour schemes
There are lots of ways of colouring Electra – David Mitchell recommends chaotic / random colouring or 5 contrasting colours. If you go for 5 colours, then the 6 modules of a particular colour form the corners of an octahedron – a beautiful, hidden symmetry that might have tickled Dürer or Escher, it certainly surprised me.
For the assembly, there’s a simple rule – make a ring of 5 modules, then add modules to make rings of three around them, then 5-rings around the 3’s and so on... For the 5 colour version, you also have to make sure that the colour on the corner of a 5-ring matches that on the opposite corner of a 3-ring.
Once the first model was made, I experimented with changing the outside of the modules – over on Thingiverse there’s a spherical version, amongst others. Or we can be more colorful, changing the filament colour after, say, 25%, 50% & 75% of printing; for example, here are some three-color modules:
And the resulting 3-color Stripey Electra!
Conclusions
To sum up – origami and 3D printing do mix. Both can produce beautiful mathematical models - but Murphy’s law rules and it sometimes takes perseverance and practice. Oh, and a tame mathematician is always useful. :)
Thanks to David Mitchell, Electra now comes in two flavours – the 30 module vanilla shown here; and twice as much fun “Electra 60” - based around a rhombicosidodecahedron with triangles, squares and pentagons. This is where paper beats plastic – paper will happily cope with changes in the module angles… but I can’t!
Acknowledgments
A big thank-you to Laura Taalman for her fascinating blog and inspirational models – and for inviting me to be a guest blogger. Also to David Mitchell for his beautiful models and origami books.
References
David Mitchell’s “Electra” http://freespace.virgin.net/dave.mitchell/galleriesmodulardesigns.htm
David Mitchell, "Paper Crystals”, 2nd edition, http://www.amazon.co.uk/dp/0953477495 or www.amazon.com/dp/0953477495
David Mitchell, “Mathematical Origami: Geometrical Shapes by Paper Folding”, www.amazon.com/dp/189961818X
Kunihiko Kasahara’s “Origami Omnibus”, www.amazon.com/dp/4817090014
My 3D printed version of Electra, http://www.thingiverse.com/thing:127857
The British Origami society, http://www.britishorigami.info/
Origami USA, https://origamiusa.org/
